La retta passante per l’origine

In questa lezione studiamo la retta, elemento geometrico fondamentale per comprendere altri argomenti più complessi. In fondo all’articolo potete visualizzare il video.

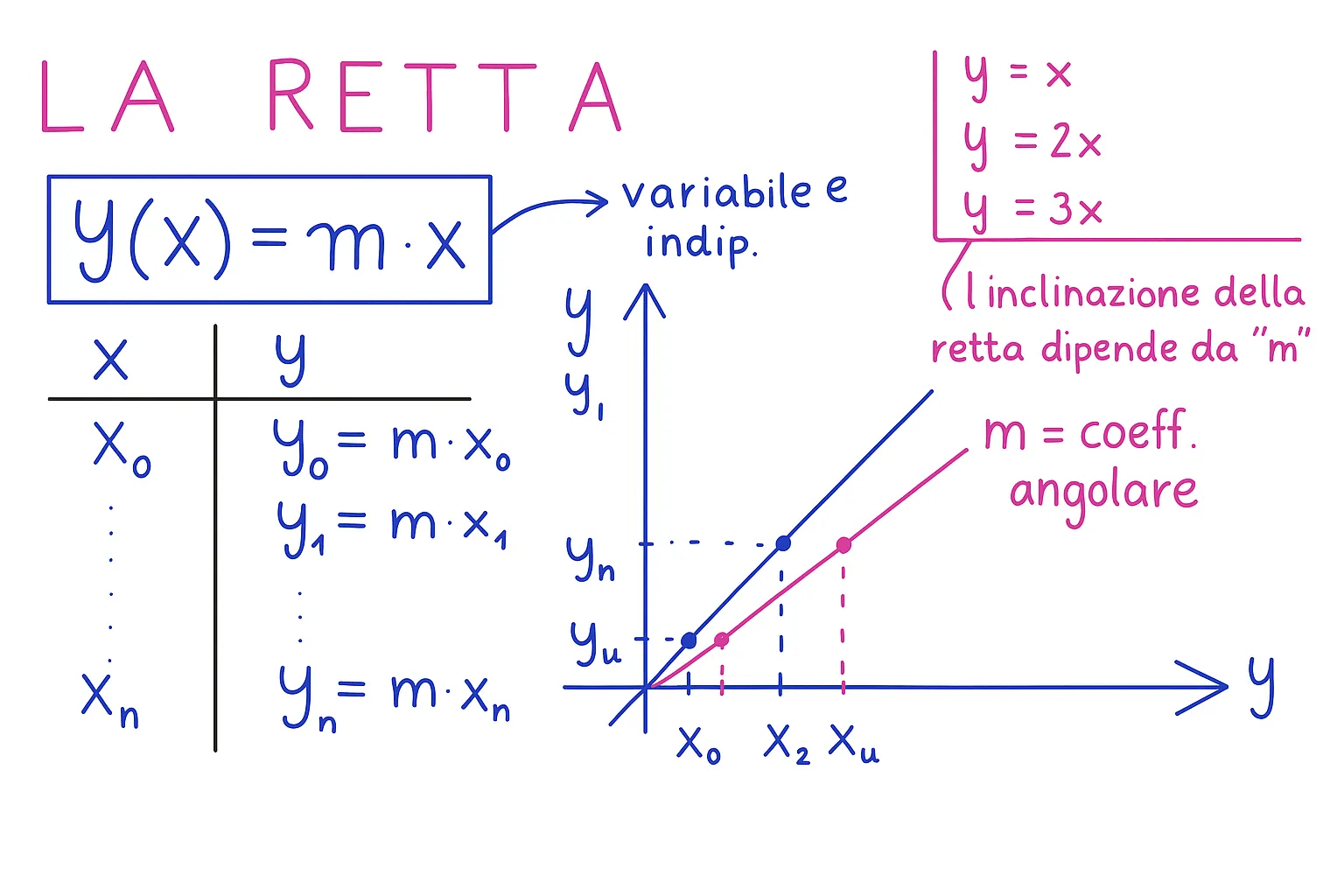
Nello studio della geometria analitica, uno dei concetti fondamentali che incontriamo è quello di retta nel piano cartesiano. Tra tutte le rette ricordiamo le rette che passano per l’origine degli assi, cioè per il punto (0,0).

Table of Contents

1. Richiamo sul piano cartesiano

E’ fondamentale fare un piccolo ripasso del piano cartesiano prima di procedere con la spiegazione delle rette. Il piano cartesiano è formato da due rette perpendicolari tra loro che si intersecano in un punto: l’origine. L’asse orizzontale si chiama asse delle ascisse (x), mentre quello verticale si chiama asse delle ordinate (y). Ogni punto nel piano può essere individuato da una coppia ordinata (x, y).

Quando rappresentiamo una retta nel piano cartesiano, lo facciamo anche analiticamente scrivendo la sua equazione:

$y = ax + q$

dove:

a è il coefficiente angolare, cioè la pendenza della retta;
q è l’ordinata corrispondente all’origine (quando x=0), ossia il punto in cui la retta interseca l’asse delle ordinate.

2. Il caso particolare: retta passante per l’origine

Se la retta passa proprio per l’origine (0,0), vuol dire che in quell’equazione il punto (0,0) deve appartenere alla retta.

Verifichiamolo:

$y =a + q$

Sostituiamo (0,0):

$0 = m \cdot 0 + q \quad \Rightarrow \quad q = 0$

Quindi, se la retta passa per l’origine, il termine noto q deve essere uguale a zero. L’equazione si semplifica in:

$y = ax$

3. Interpretazione geometrica del coefficiente angolare

Il parametro a (coefficiente angolare) ha un ruolo cruciale: determina l’inclinazione della retta.

Se a > 0, la retta sale da sinistra verso destra.
Se a < 0, la retta scende da sinistra verso destra.
Se a = 0, la retta coincide con l’asse delle ascisse (orizzontale).
Se la retta è verticale (cioè parallela all’asse y), non può essere scritta come $y = mx$ , perché il coefficiente angolare sarebbe “infinito”. In quel caso l’equazione è $x = 0$ , che rappresenta l’asse delle ordinate.

Quindi, tranne per la retta verticale, ogni retta passante per l’origine è descritta dalla formula $y = mx$ .

4. Esempi pratici

Esempio 1: $y = 2x$
Significa che a ogni incremento di 1 unità in x, la y aumenta di 2. La retta passa per (0,0), (1,2), (2,4)…
Esempio 2: $y = -\tfrac{1}{2}x$
Qui la pendenza è negativa. A ogni incremento di 2 unità in x, la y diminuisce di 1. La retta passa per (0,0), (2,-1), (4,-2)…
Esempio 3: $y = 0 \cdot x, cioè y = 0$
La retta coincide con l’asse x.

5. Rette passanti per l’origine come proporzionalità diretta

C’è un aspetto molto interessante: l’equazione $y =$ rappresenta una proporzionalità diretta.

Infatti:

$\frac{y}{x} = m$

Significa che il rapporto tra y e x è sempre costante, uguale al coefficiente angolare.

Le rette sono spesso usate in fisica o economia per rappresentare fenomeni proporzionali (per esempio, lo spazio percorso in funzione del tempo a velocità costante).

6. Connessione con la trigonometria

Il coefficiente angolare a è collegato anche all’angolo di inclinazione α della retta rispetto all’asse x. Vale infatti la relazione:

$m = \tan(\alpha)$

Se l’angolo α è acuto (tra 0° e 90°), la tangente è positiva, quindi la retta ha pendenza positiva.
Se l’angolo è ottuso (tra 90° e 180°), la tangente è negativa e la retta scende.

Questa connessione tra geometria analitica e trigonometria è molto utile per calcolare inclinazioni e per passare da rappresentazioni algebriche a rappresentazioni grafiche.

7. Conclusione

Le rette passanti per l’origine costituiscono una delle famiglie di rette più semplici da descrivere, ma anche tra le più importanti. Esse hanno equazione della forma $y =ax$ , dove a rappresenta il coefficiente angolare, cioè la pendenza.

Il loro studio permette di comprendere concetti chiave come:

la relazione tra equazione e grafico;
la proporzionalità diretta;
il legame con la trigonometria (tangente dell’angolo).

Inoltre, hanno applicazioni pratiche in molti campi: dalla fisica (velocità costante, leggi lineari), all’economia (costi proporzionali), fino all’informatica (grafici e algoritmi di computer graphics).

Capire bene la retta passante per l’origine significa gettare le basi per lo studio di tutte le altre funzioni lineari e, più in generale, dell’analisi matematica.