Lezione di Fisica: Introduzione alla Cinematica
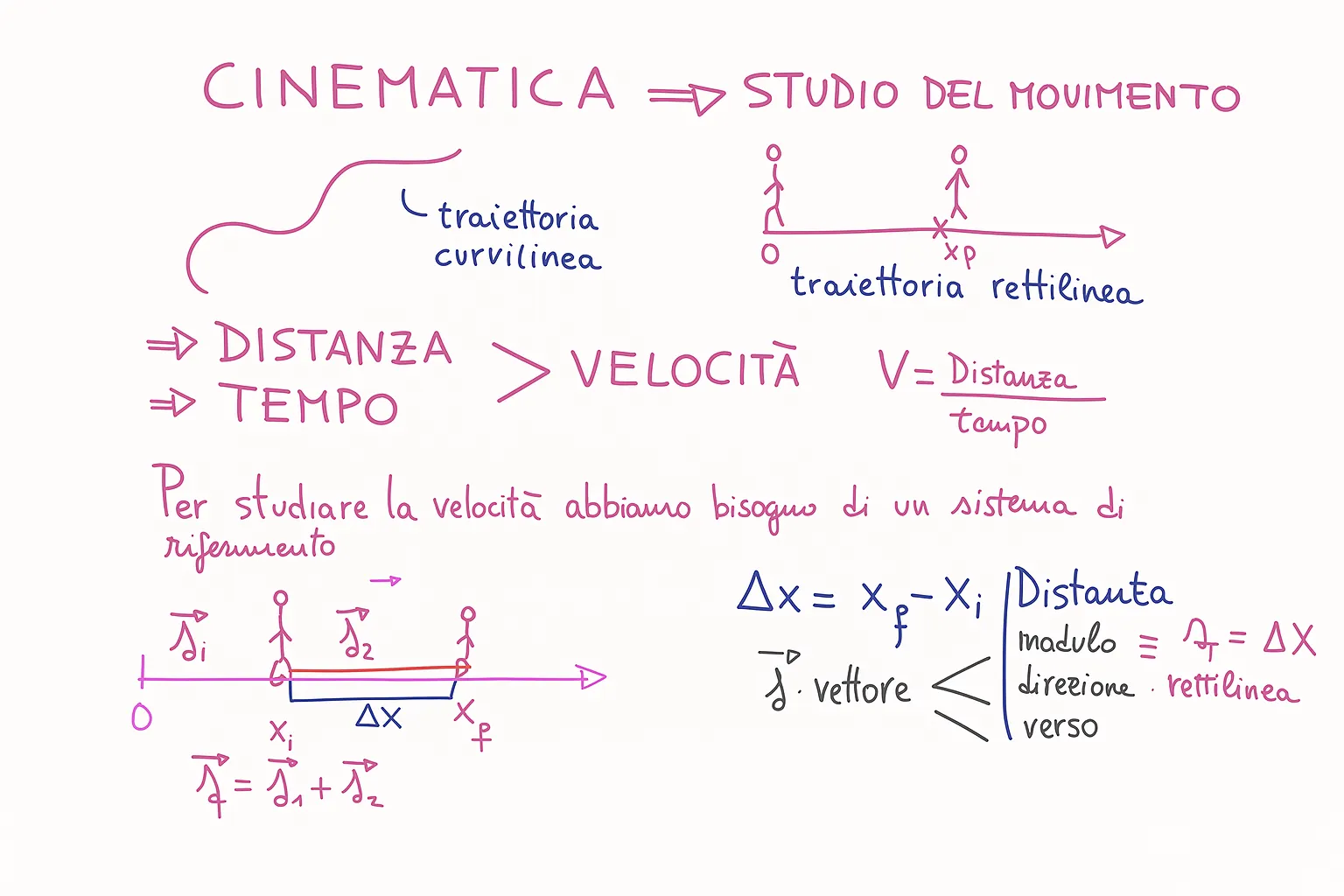
La cinematica è la parte della fisica che studia il moto dei corpi, cioè come gli oggetti si muovono nello spazio e nel tempo, senza preoccuparsi delle cause che producono il movimento.
In altre parole, la cinematica descrive il “come” del moto, mentre la dinamica si occupa del “perché” un corpo si muove.
Comprendere la cinematica è fondamentale perché ci permette di analizzare, prevedere e rappresentare graficamente il comportamento di un oggetto in movimento.
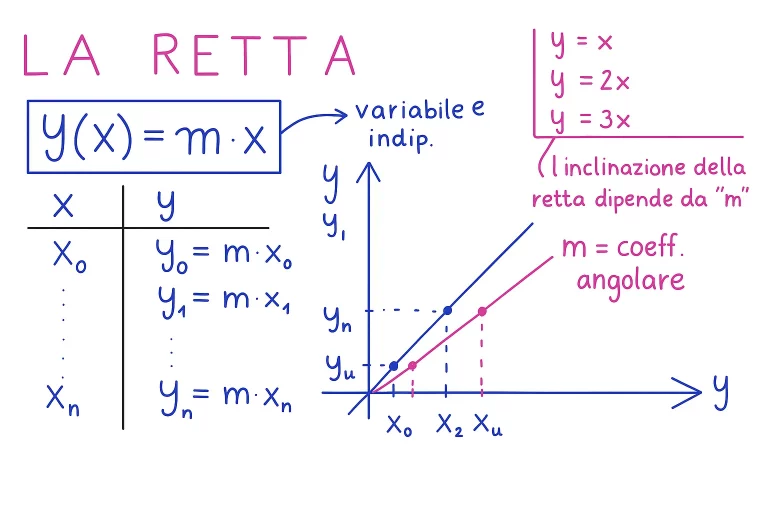
Per descrivere un moto, il primo concetto che dobbiamo introdurre è quello di posizione. La posizione di un corpo è il punto in cui esso si trova rispetto a un sistema di riferimento scelto, che può essere ad esempio una linea retta se studiamo un moto unidimensionale (vedi figura). La posizione è la base su cui possiamo calcolare altre grandezze importanti come lo spostamento e la velocità.
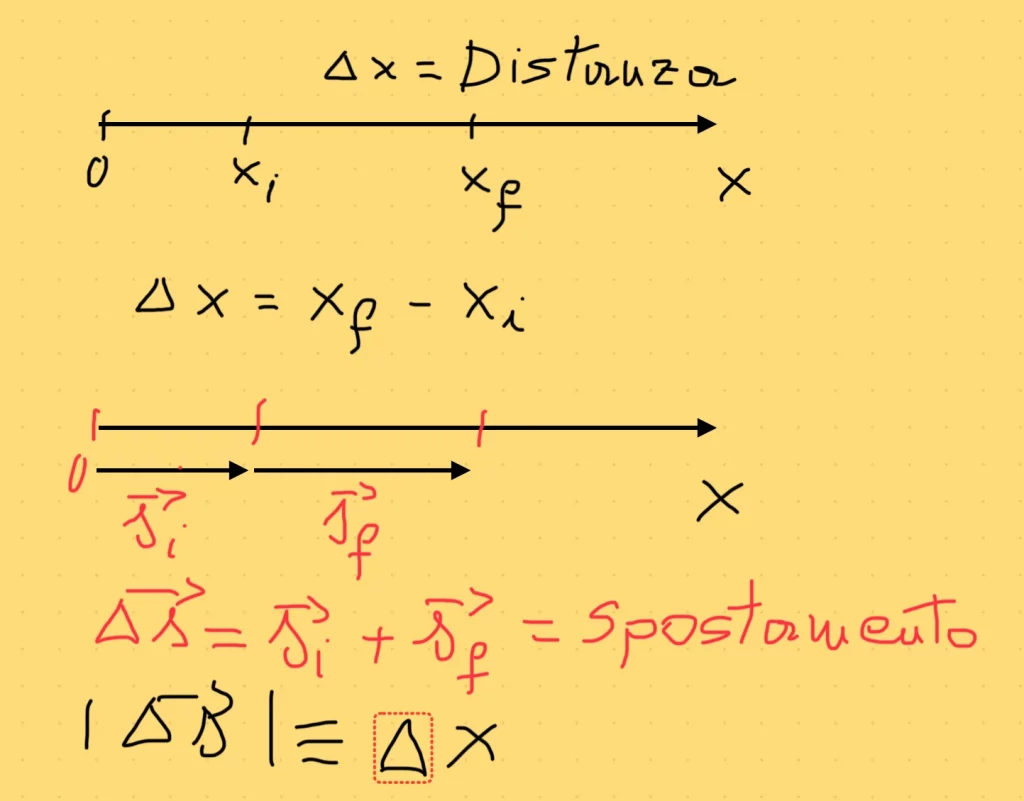
Quando un oggetto si muove, possiamo misurare due quantità diverse: la distanza percorsa e lo spostamento. La distanza è una grandezza scalare e rappresenta la lunghezza effettiva del percorso compiuto, senza tener conto della direzione. Lo spostamento, invece, è un vettore, cioè una grandezza che è caratterizzata oltre che dal modulo (lunghezza del vettore), anche dalla direzione e dal verso, e indica la distanza più breve tra il punto iniziale e quello finale del percorso. Ad esempio, se un ciclista parte da casa, fa un giro di due chilometri e torna a casa, la distanza percorsa sarà di 2 km, mentre lo spostamento sarà zero, perché il punto iniziale e quello finale coincidono. Questa differenza tra distanza e spostamento è fondamentale per comprendere come descrivere correttamente un moto.
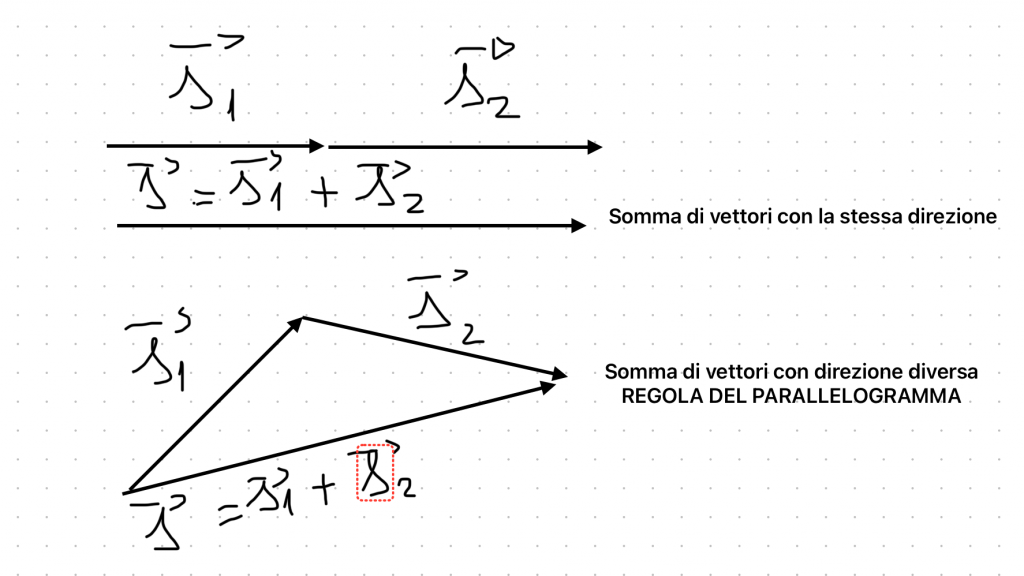
A questo punto è utile ricordare brevemente cosa sono i vettori. Un vettore è un elemento matematico che rappresenta una quantità con direzione e verso, come lo spostamento, la velocità o la forza. La somma di due vettori non si fa semplicemente sommando i valori numerici, ma richiede di considerare direzione e verso. Ad esempio, per sommare due spostamenti possiamo usare la regola del parallelogramma: poniamo i due vettori con la stessa origine, completiamo il parallelogramma e il vettore diagonale rappresenterà lo spostamento totale. Un’altra possibilità è sommare le componenti dei vettori lungo gli assi cartesiani, metodo particolarmente utile in problemi più complessi.
Un’altra grandezza fondamentale in cinematica è la velocità. La velocità misura quanto rapidamente e in quale direzione un corpo si sposta. Nel caso di un moto rettilineo, possiamo definire la velocità media come il rapporto tra lo spostamento Δx e l’intervallo di tempo Δt impiegato:
Se la velocità rimane costante nel tempo, il moto è detto uniforme, e la posizione in un certo istante può essere calcolata facilmente usando la formula:
dove 
è la posizione iniziale. La velocità, essendo un vettore, non indica solo quanto velocemente si muove un corpo, ma anche in quale direzione. In caso di variazioni della velocità, si introduce invece il concetto di accelerazione, che analizzeremo nei prossimi incontri.
È importante collegare questi concetti con esempi pratici. Ad esempio, immaginate una macchina che percorre una strada dritta. Se la macchina parte dal chilometro 0 e arriva al chilometro 100, la distanza percorsa è 100 km, e lo spostamento, se la partenza e l’arrivo coincidono con la stessa direzione, sarà anch’esso di 100 km. Se invece la macchina fa un percorso ad anello e torna al punto di partenza, la distanza percorsa può essere molto grande, ma lo spostamento sarà zero. Questi esempi aiutano a capire come la direzione influisca sulla descrizione del moto.
In sintesi, la cinematica ci permette di descrivere e prevedere i movimenti dei corpi utilizzando concetti fondamentali come posizione, distanza, spostamento e velocità. Questi strumenti matematici e concettuali sono essenziali per affrontare problemi più complessi, come moti curvilinei o accelerati, e costituiscono la base per tutta la fisica del movimento. Nei prossimi incontri approfondiremo la velocità istantanea e l’accelerazione, introducendo anche le rappresentazioni grafiche dei moti, che ci aiuteranno a visualizzare meglio come cambiano le grandezze nel tempo.
Sull'autore
